En el artículo anterior hablé sobre la tasa de referencia, que es el costo que los gobiernos aceptan pagar por la emisión de sus títulos de deuda y que sirven para establecer otras tasas de interés. Pues bien, las tasas de interés son exactamente eso, es el costo del dinero.
Si ustedes realizan una inversión, la tasa de interés va a ser el rendimiento o valor que van a recibir adicional como resultado de su inversión y si ustedes solicitan un préstamo, la tasa de interés juega en contra y representa el costo que tendrán que pagar por usar el dinero prestado.
En el mundo de las finanzas, existen dos tipos de tasas de interés, el interés simple y el interés compuesto.
En el interés simple el valor resultante del cálculo no afecta al valor inicial del capital, por lo tanto los intereses siempre van a ser los mismos. En contraposición, en el interés compuesto, el resultado del cálculo es sumado al capital inicial y por lo tanto afecta el resultado del interés del próximo periodo.
Vamos a ver eso con algunos ejemplos:
Si realizamos una inversión de 10.000 dólares a una tasa de interés simple del 6% al año con capitalización anual por un lapso de 5 años, tendríamos los siguientes resultados:
| Año | Capital Inicial | Tasa de Interés | Interés Generado | Saldo Final |
| 1 | 10.000 | 6% | 600 | 10.600 |
| 2 | 10.000 | 6% | 600 | 11.200 |
| 3 | 10.000 | 6% | 600 | 11.800 |
| 4 | 10.000 | 6% | 600 | 12.400 |
| 5 | 10.000 | 6% | 600 | 13.000 |
Si realizamos el mismo ejercicio utilizando el interés compuesto tendríamos los siguientes resultados:
| Año | Capital Inicial | Tasa de Interés | Interés Generado | Saldo Final |
| 1 | 10.000 | 6% | 600 | 10.600 |
| 2 | 10.600 | 6% | 636 | 11.236 |
| 3 | 11.236 | 6% | 674,16 | 11.910,16 |
| 4 | 11.910,16 | 6% | 714,61 | 12.624,77 |
| 5 | 12.624,77 | 6% | 757,49 | 13.382,26 |
Como pueden ver, el interés compuesto acelera los resultados y el efecto es más notable a medida que el plazo es más largo, por ejemplo si repetimos el ejemplo, pero con un plazo de 30 años, tendríamos lo siguiente:
Interés simple:
| Año | Capital Inicial | Tasa de Interés | Interés Generado | Saldo Final |
| 1 | 10.000 | 6% | 600 | 10.600 |
| 2 | 10.000 | 6% | 600 | 11.200 |
| 3 | 10.000 | 6% | 600 | 11.800 |
| …. | …. | …. | …. | …. |
| 28 | 10.000 | 6% | 600 | 26.800 |
| 29 | 10.000 | 6% | 600 | 27.400 |
| 30 | 10.000 | 6% | 600 | 28.000 |
Aplicando el interés compuesto, el resultado seria el siguiente:
| Año | Capital Inicial | Tasa de Interés | Interés Generado | Saldo Final |
| 1 | 10.000 | 6% | 600 | 10.600 |
| 2 | 10.600 | 6% | 636 | 11.236 |
| 3 | 11.236 | 6% | 674,16 | 11.910,16 |
| …. | …. | …. | …. | …. |
| 28 | 48.223,46 | 6% | 2.893,41 | 51.116,87 |
| 29 | 51.116,87 | 6% | 3.067,01 | 54.183,88 |
| 30 | 54.183,88 | 6% | 3.251,03 | 57.434,91 |
Como pueden ver el valor final del interés compuesto es de 57.434,91 que comparado con los 28.000 del interés simple es mucho mayor, es prácticamente un poco más del doble.
¿De dónde salen esos números?
Las fórmulas para interés simple e interés compuesto son las siguientes:
Fórmula de interés simple:

Fórmula de interés compuesto:
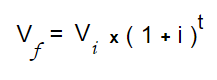
Como les comenté al inicio, el tiempo tiene un efecto exponencial cuando se calcula el interés compuesto, por ese motivo, cuando se solicita un crédito a muy largo plazo, se terminan pagando muchos intereses y por ese mismo motivo las inversiones a largo plazo son más rentables que las inversiones a corto plazo.
¿Qué pasa si la capitalización se hace mensualmente y no anualmente?
En los ejemplos anteriores se mostró la capitalización de forma anual, pero qué pasa cuando la capitalización se realiza en diferentes períodos, por ejemplo mensual o diario, para saber eso, primero debemos aprender como calcular las tasas de interés equivalentes porque si ustedes dividen la tasa anual entre 12 estarán cometiendo un gran error, veamos la siguiente fórmula:

La tasa mensual equivalente a 6% anual seria calculada de la siguiente forma:
Tasa equivalente = (( 1 + 6%)^(1/12)) – 1
Tasa equivalente = (( 1,06)^0,0833333)) – 1
Tasa equivalente = 1,04867551 – 1
Tasa equivalente = 0,004867550565
Tasa equivalente = 0,4867550565%
Como pueden ver existe una pequeña diferencia entre esa tasa equivalente y el resultado de dividir la tasa anual entre 12, lo cual daría 0,5%.
Eso se explica, porque en el interés compuesto, el resultado de los intereses se acumulan y afectan el capital, como ya habíamos visto y el efecto no es lineal.
Si aplicamos la fórmula de Interés compuesto: Vf= C * (( 1 + i )^t) a nuestro ejemplo de 30 años que tenemos exactamente el mismo resultado:
Vf = 10.000 * (( 1 + 0,004867550565)^360)
Dónde 360 meses, corresponden a 30 años.
Tenemos como resultado: 57.434,91
Ahora Imaginense si a esto le sumamos aportes mensuales o anuales al capital inicial, el efecto multiplicador es mucho mayor, veamos un ejemplo:
Si realizamos una inversión inicial de 10.000 dólares, y realizamos aportes mensuales de 350 dólares a una tasa de interés del 6% anual (equivalentes a 0,4867550565% al més), con capitalización mensual durante 30 años (360 meses), al final tendríamos 468.418,72 dólares en nuestra cuenta lo cual es significativamente mayor.
Ese es el efecto poderoso de realizar aportes mensuales a su inversión, aunque sean aportes pequeños.
¿Cómo se realiza ese cálculo?
La fórmula para calcular el resultado considerando los aportes mensuales sería la siguiente:
Monto final = Inversión inicial * (1 + Tasa de interés mensual)^Número de meses + Aporte mensual * (((1 + Tasa de interés mensual)^Número de meses – 1) / (Tasa de interés mensual))
Podemos dividir esta fórmula en dos partes, la primera encuentra el valor futuro de la inversión inicial (VFII)
VFII = Inversión inicial * (1 + Tasa de interés mensual)^Número de meses
y la segunda parte encuentra el valor futuro de los aportes mensuales acumulados (VFAM)
VFAM = Aporte mensual * (((1 + Tasa de interés mensual)^Número de meses – 1) / (Tasa de interés mensual))
Parámetros:
Inversión inicial: $10.000
Aporte mensual: $350
Capitalización: Mensual
Tasa de interés mensual: 0.4867550565% (equivalente a un 6% anual)
Periodo de tiempo: 30 años
Fórmula:
Así como en el ejemplo anterior, el valor futuro de la inversión inicial es de: 57.434,91 lo interesante ocurre cuando sumamos el valor futuro de los aportes mensuales:
VFAM = 350 * ((( 1 + 0,004867550565)^359)/(0,004867550565)) = 410.983,81
Si sumamos los resultados tenemos: 468.418,72
Hasta aquí todo bien, podemos ver que el interés compuesto y los aportes mensuales hasta el momento son los héroes, pero…
¿Cuándo se convierten en Villanos?
Imagine que Usted necesita dinero y lo pide prestado a un Banco o peor aún, usa su tarjeta de crédito, en ese caso, el interés compuesto comienza a trabajar en contra suya, si por casualidad decide usar el financiamiento.
Con el agravante de que las tasas de interés que cobran los bancos o los emisores de las tarjetas de crédito son absurdamente más altas que las ofrecidas como remuneración de su dinero.
En los Estados Unidos, existen empresas que ofrecen tarjetas de crédito con intereses anuales (APR) “reducidos” del 17,99% al año lo que equivale a 1.39% mensual, y lo normal es ver empresas que cobran hasta 29.99% al año, equivalentes a 2.21% mensual.
En Brasil el escenario es todavía peor, porque las tasas de interés que pueden cobrar los emisores de tarjetas de crédito, exceden fácilmente el 445% al año, equivalentes a 15.18% al mes.
Recientemente en Brasil fue aplicado un programa que limita los intereses cobrados por deudas de tarjetas de crédito hasta un 100% del valor solicitado.
Viendo esos intereses y aplicando las fórmulas mostradas en este artículo, pueden darse cuenta que cuando se trata de préstamos, las tasas de interés son los verdaderos villanos de la historia.



